Support Vector Machine (Statistics)

The master bioinformatics offers the chance to get acquainted to several machine learning techniques. Machine learning algorithms are used in various courses, the theoretical ground work is taught in statistics. There we repeat how linear regression and hidden markov machines work, learning more about the mathematical concept of markov chains, and we get introduced to support vector machines (SVMs) and how to make them more efficient using the kernel trick.

SVMs are supervised learning models usually used on very large data sets which you want to divide into two classes. The division is performed by laying a plane or hyperplane between the two classes and maximizing the distance to each of them. If the classes are not linearly separable you have to transform the input space with a transformation function, called phi here, which introduces more dimensions. This function phi has to be cleverly chosen such that the two classes get cleanly separated without introducing too many new dimensions. Of course if you add enough dimensions everything can become separable, even if in reality there are no features distinguishing them. Another problem with adding too many dimensions is overfitting (learning properties of single data points instead of general class properties). Even when it does make sense to introduce this many new dimensions you will end up running into the curse of dimensionality. For with every new dimension the input points end up further apart from each other until the data is so sparse that the positioning of the dividing hyper plane becomes in a way arbitrary, which of course compromises your results when trying to classify new points.

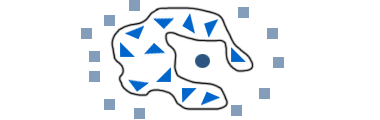
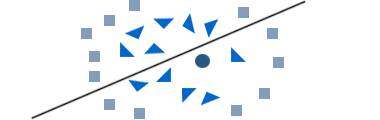
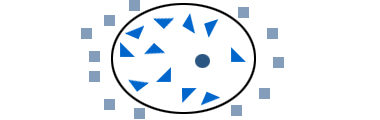
Match the functions used for transforming the input space to the resulting decision borders. x=(x₁,x₂)