Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Das Kartenspiel SET oder Geraden im affinen Raum
Set ist ein Kartenspiel, das 1974 von Marsha Jean Falco im Rahmen ihrer Forschung zur Genetik in Cambridge erfunden wurde. Um die Masse der genetischen Informationen übersichtlicher zu gestalten, beschrieb sie diese durch Symbole, die deren Eigenschaften in verschiedenen Variationen codierten. Sie schrieb diese auf Karten und bei dem Versuch, Kollegen die Zusammenhänge zu beschreiben, entstand dieses Spiel. Es ist seit 1991 im Handel und hat diverse Auszeichnungen erhalten und ist mittlerweile auch in verschiedenen Versionen als App verfügbar.
Kartenmotive
Das Spielmaterial besteht ausschließlich aus Karten, bedruckt mit Symbolen, die genau eine Eigenschaft in einer Variante aufweist.
| Eigenschaften | Varianten |
|---|---|
| Farbe | rot, grün, blau |
| Form | oval, rechteckig, rautenförmig |
| Füllung | leer, schraffiert, voll |
| Anzahl | eins, zwei, drei |
Zu jeder Kombination gibt es genau eine Karte.
Spielregeln
Ziel des Spiels ist es, möglichst viele Sets zu ergattern. Was ist ein Set? Ein Set besteht aus drei Karten, die bezogen auf eine Eigenschaft, entweder alle dieselbe Variante oder komplett verschiedenen Varianten aufweisen. Es werden 12 Karten ausgelegt (siehe Abbildung) und derjenige, der zuerst ein Set entdeckt und auch „Set“ ruft, darf das Tripel an sich nehmen. Die Karten werden wieder auf 12 ergänzt. Sollte sich unter den 12 ausgelegten Karten kein Set befinden, so wird die Auslage um zusätzliche drei Karten erweitert und so fährt man fort bis wieder ein Set dabei ist. Sind alle Karten aufgebraucht, gewinnt der/die SpielerIn mit den meisten Karten.
1. Aufgabe
Bitte beantworten Sie mit Hilfe der o.g. Informationen die folgenden Fragen:
Aus wievielen Karten besteht das Kartenspiel insgesamt?
Da es zu jeder Kombination der Eigenschaften mit einer Variation genau eine entsprechende Karte gibt, kommt man auf 81 = 3 · 3 · 3 · 3 verschiedenen Karten.
Aus mathematischer Sicht entspricht eine Karte einem Vektor im vierdimensionalen Vektorraum über dem Körper mit drei Elementen
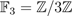
wir erhalten somit den Vektorraum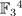 
.
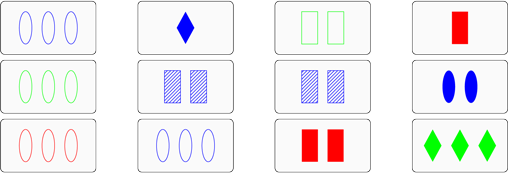
Wieviele verschiedene Sets sind in der abgebildeten Auslage verborgen (Überschneidungen sind erlaubt)?
Es gibt sogar vier verschiedene Sets in dieser Auswahl.
Wieviele Karten muss man mindestens auslegen, damit garantiert ein Set dabei ist?
Es sind 21 Karten und das ist gar nicht so einfach zu beweisen.
Reduziert man die Anzahl der Eigenschaften auf drei, so benötigt man mindestens 10 Karten und bei zwei Dimensionen reduziert es sich auf 5 Karten, was man auch graphisch sehr schön darstellen kann:
Die 9 Karten entsprechen dabei den 9 Punkten in der Ebene: {(x, y) : x, y = 0, 1, 2} und die Geraden tatsächlich den Geraden im Raum, eindeutig bestimmt durch zwei Punkte. Die blauen Kreise geben eine maximale Anzahl von Punkten, so dass keine drei Punkte auf einer Geraden liegen. Jeder weitere Punkt würde eine Gerade vervollständigen.
Erhöht man jedoch die Anzahl der Eigenschaften, oder äquivalent die Dimension des Vektorraums, so weiß man noch bei sechs Dimensionen, dass 46 Karten benötigt werden, jedoch ab Dimension 7 ist die Frage weiterhin offen. Siehe dazu auch The Card Game SET von Benjamin Lent Davis, Diane Maclagan und Ravi Vakil.
Sie erhalten ein Feedback zu den einzelnen Antworten, indem Sie auf das klicken.
2. Aufgabe
In der folgenden Abbildung sehen Sie vier unvollständige Sets, bei denen jeweils eine Karte fehlt. Versuchen Sie per drag-and-drop die jeweils fehlende Karte in den Sets durch die vier Karten am rechten Rand zu ergänzen.
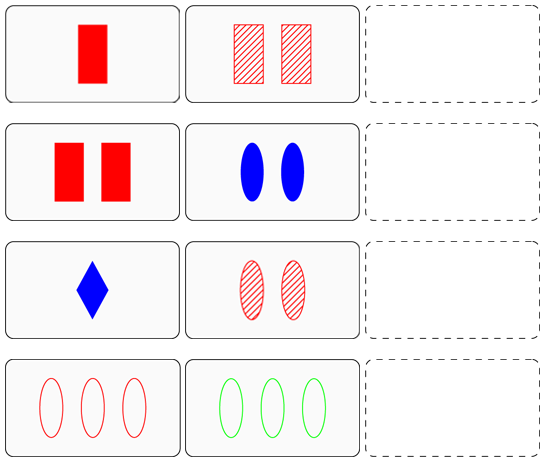
Diese Karte vervollständigt die zweite Reihe zu einem Set, da dort die beiden gegebenen Karten in Anzahl und Füllung übereinstimmen, daher muss auch die gesuchte dritte Karte zwei gefüllte Figuren haben. Jedoch in Farbe und Form sind sie verschieden, also muss die dritte Karte die jeweils dritte Variante bezüglich dieser Eigenschaften aufweisen, sprich grüne Rauten.
Diese Karte vervollständigt die vierte Reihe zu einem Set, da dort die beiden gegebenen Karten in Anzahl, Form und Füllung übereinstimmen und daher auch die gesuchte dritte Karte drei leere Ellipsen haben muss. In der Farbe jedoch sind sie verschieden, also muss die dritte Karte die dritte Variante bezüglich dieser Eigenschaft aufweisen, sprich blau.
Diese Karte vervollständigt die dritte Reihe zu einem Set, da dort die beiden gegebenen Karten in keiner Eigenschaft übereinstimmen. Also muss die dritte Karte die jeweils dritte Variante bezüglich der entsprechenden Eigenschaft aufweisen. Wir erhalten also in der dritten Reihe drei grüne, leere Rechtecke.
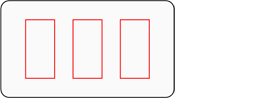
Diese Karte vervollständigt die erste Reihe zu einem Set, da dort die beiden gegebenen Karten in Farbe und Form übereinstimmen und damit auch die gesuchte dritte Karte rote Rechtecke haben muss. Jedoch in Anzahl und Füllung sind sie verschieden, also muss die dritte Karte die jeweils dritte Variante bezüglich dieser Eigenschaften aufweisen: sprich drei und leer.
Sie erhalten ein Feedback zu den einzelnen Antworten, indem Sie auf das klicken.