Mathematische Logik

Was ist ein mathematischer Beweis? Wie lassen sich Beweise rechtfertigen? Gibt es Grenzen der Beweisbarkeit? Ist die Mathematik widerspruchsfrei? Kann man das Auffinden mathematischer Beweise Computern übertragen?

Erst im 20.Jahrhundert ist es der mathematischen Logik gelungen, weitreichende Antworten auf diese Fragen zu geben. Grundlage dafür ist eine formale Sprache, bestehend aus einem Alphabet und daraus gebildeten Wörtern (A,B,C...) , genannt Aussagen - die formalen Bildungsgesetze sollen uns hier nicht beschäftigen. Insbesondere soll unser Alphabet neben Variablen und Klammern (,) auch folgende Symbole (genannt Junktoren) beinhalten:

Negation: ¬ (gesprochen „nicht”)
Konjunktion: ∧ (gesprochen „und”)
Disjunktion: ∨ (gesprochen „oder“)
Implikation: → (gesprochen „wenn... , dann” oder „impliziert”)
Äquivalenz: ↔ (gesprochen „genau dann wenn” oder „aquivalent zu”)

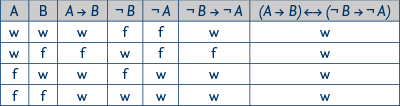
Ordnet man einer Aussage einen Wahrheitswert zu, w soll dabei für „wahr“ stehen und f für „falsch“, so kann man Mithilfe von Wahrheitstafeln die Bedeutung der Junktoren festlegen – siehe Abbildung.

Ordne ich zum Beispiel der Aussage A den Wahrheitswert w zu, der Aussage B den Wahrheitswert f , so hat die Aussage AvB laut Tabelle den Wahrheitswert w, hingegen A∧B, A→B und A↔B als auch ¬A den Wahrheitswert f.

Formalisierung der Mathematik - Grenzen und Chancen

Der obige Formalismus ist bekannt als Aussagenlogik. Die Beweisbarkeit in dieser Logik ist mit einem Computer entscheidbar. Als Grundlage für die Mathematik ist die Aussagenlogik jedoch aufgrund ihrer mangelnden Ausdrucksstärke nicht geeignet; ausdrucksstärkere Formalismen sind hierzu erforderlich.

Ein geeigneter erster Ansatz ist die axiomatische Mengentheorie in der Logik erster Stufe. Sie erweitert den obigen Formalismus um eine reichhaltige Termsprache (basierend auf Funktions-, Relations- und Konstantensymbolen) und stellt, zusätzlich zu den obigen Junktoren, All- und Existenzquantoren zur Verfügung. Damit lassen sich bereits viele mathematische Axiome und Theoreme formalisieren.
Die Logik erster Stufe ist nicht mehr entscheidbar, jedoch zeigt Gödel's Vollständigkeitssatz, dass man Beweissysteme bereitstellen kann, mit denen jeder gültige Satz der Logik ersten Stufe theoretisch auch als solcher formal bewiesen werden kann.
Solche Beweissysteme wurden bereits auf dem Computer implementiert; zu den bekanntesten erststufigen Theorembeweisern gehören Vampire, Eprover und Spass.

Um jedoch komplexere Theorien in der Mathematik elegant und angemessen darzustellen, benötigt man ausdrucksstärkere Sprachen - diese bezeichnet man als Logik höherer Stufe. Sie lässt z.B. All- und Existenzaussagen auch über Funktionen und Relationen zu ("Für alle Funktionen F gilt, ..." bzw. "Für alle Relationen R gilt, ...").
Gödel's Unvollständigkeitssätze zeigen aber, dass die Logik höherer Stufe grundsätzlich unvollständig ist - das bedeutet, man kann kein Beweissystem angeben, mit dem sich alle gültigen Aussagen der Logik höherer Stufe auch formal ableiten lassen. Ein überwiegender Teil mathematisch relevanter Fragestellungen kann aber dennoch mit dem Formalismus der Logik höherer Stufe formal analysiert werden. Die Mächtigkeit dieser Formalisierung illustriert zum Beispiel der formale Beweis durch Thomas Hales, der besagt, dass die Kepler'sche Vermutung zur optimalen Anordnung von Kugelpackungen im dreidimensionalen euklidischen Raum richtig ist. Traditionell arbeitende Mathematiker waren zuvor an der Verifikation dieses Beweises gescheitert. Lesenswerte Presseartikel dazu finden Sie bei Spiegel-Online oder eine etwas kritischere Sichtweise hierzu auch bei Quantamagazine.
Bekannte Beweissysteme für die Logik höherer Stufe (und darauf aufbauende Typentheorien) sind, Isabelle/HOL, Coq, HOL und HOL-light. An der FU Berlin wird der automatische höherstufige Beweiser LEO-III entwickelt.

Tautologie und Kontradiktion

Eine Tautologie ist eine allgemeingültige Aussage, wie zum Beispiel „Es regnet oder es regnet nicht”. Hingegen eine Kontradiktion bezeichnet eine stets falsche Aussage bzw. einen Widerspruch in sich, hier zum Beispiel „Es regnet und es regnet nicht”.

In unserer formalen Sprache entspricht eine Tautologie einer Aussage, deren Wahrheitswert immer „wahr” ist, eine Kontradiktion hingegen hat immer den Wert „falsch” - unabhängig vom Wahrheitsgehalt ihrer Teilaussagen.

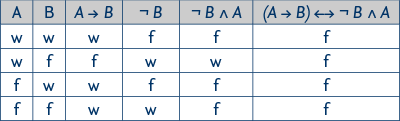
Überprüfen lässt sich dies am Einfachsten durch Erstellen von Wahrheitstafeln. So erhalten wir für die Aussage A =„Es regnet” und die oben genannten Beispiele folgende Wahrheitstafeln:

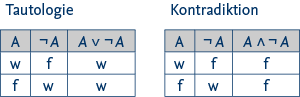
Welche der folgenden Aussagen ist eine Tautologie, eine Kontradiktion oder keines von beiden? Dabei bindet die Negation stärker als die Konjunktion und Disjunktion und diese wiederum stärker als die Implikation und Äquivalenz.