Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Paradoxa
Der Begriff Paradoxon oder auch Paradoxie kommt aus dem Altgriechischen: 'para' heißt 'neben', 'außer', 'daran vorbei' und 'doxa' bedeutet 'Meinung' oder 'Ansicht' – im Plural Paradoxa oder Paradoxien. Es kann eine Aussage bezeichnen, die einen scheinbar unauflösbaren Widerspruch enthält. Ein geläufiges Beispiel ist der Barbier, der alle rasiert, die sich nicht selbst rasieren. Wer rasiert den Barbier? Ein anderes Beispiel ist „die Menge aller Mengen, die sich nicht selbst enthalten“ , die einem vor Augen führt, dass man mit dem Begriff „Menge“ nicht zu unbedarft umgehen sollte.
Oft aber auch werden mit Paradoxa Phänomene beschrieben, die sich einfach nur unserer Anschauung entziehen. Zuweilen sind es Fragen, die mit gesundem Menschenverstand durchaus lösbar sind, jedoch unserer Intuition widersprechen. Ein beliebtes Beispiel ist Hilberts Hotel: Das Hotel hat unendlich viele Zimmer, die mit 1,2,3... durchnummeriert sind. Es ist eine große Konferenz in der Stadt und alle Zimmer sind ausgebucht. Da kommt ein weiterer Gast spät abends und bittet um ein Zimmer. Was macht der Empfangschef? Er bittet den Gast in Zimmer 1 ins Zimmer 2 zu wechseln, Gast aus Zimmer 2 in Zimmer 3 zu wechseln und so weiter. Damit ist Zimmer 1 frei für den späten Gast und alle können nacheinander wieder beruhigt schlafen gehen.
Ein besonders ergiebiges Feld für Paradoxa ist auch die Wahrscheinlichkeitstheorie, dort klaffen Erwartung und mathematische Wahrheit besonders oft weit auseinander.
1. Aufgabe: Das Geburtstagsparadoxon
Die Professorin wettet in der Vorlesung mit den Studierenden, dass mindestens zwei Studierende im Hörsaal am gleichen Tag Geburtstag haben. Gemeint ist natürlich unabhängig vom Geburtsjahr und wir haben kein Schaltjahr.
Wie groß sind ihre Chancen, dass sie diese Wette gewinnt, wenn an diesem Tag 40 Studierende anwesend sind?
Für eine Person gibt es 365 Möglichkeiten, Geburtstag zu haben, für zwei schon 365 ⋅ 365 usw. Bei 40 Personen muss man die Zahl 365 schon 40 Mal mit sich selbst multiplizieren.
Wie viele von diesen Möglichkeiten führen zu einem Doppelgeburtstag? Leichter lässt sich ausrechnen, wie oft es vorkommt, dass alle Geburtstage verschieden sind. Wenn die erste Person an irgendeinem Tag Geburtstag hat (365 Möglichkeiten), so gibt es für die zweite nur noch 364 freie Tage, denn einer ist ja schon weg. Das heißt 365 ⋅ 364 Möglichkeiten, dafür, dass die beiden Geburtstage verschieden sind. Bei drei Leuten muss man schon 365 ⋅ 364 ⋅ 363 ausrechnen, und bei 40 Personen hat man 40 Faktoren zu berücksichtigen, die jeweils um Eins abnehmen. In Formeln:
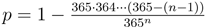
Dabei entspricht p der Wahrscheinlichkeit, dass bei n Personen mindestens zwei am selben Tag Geburtstag haben.
Für n=40 erhalten wir p=0.89, sprich eine Wahrscheinlichkeit von 89%. Bereits bei 23 Personen ist die Wahrscheinlichkeit schon knapp über 50%.
2. Aufgabe: Das Ziegenproblem
In einer Quizshow soll in der Endrunde der Kandidat eine von drei Türen wählen. Hinter einer Tür ist der Hauptgewinn (ein Auto) und hinter den beiden anderen jeweils eine Ziege. Der Kandidat wählt erst eine Tür ohne sie zu öffnen, danach öffnet der Quizmaster eine andere Tür, hinter der eine Ziege steht. Jetzt hat der Kandidat nochmals die Möglichkeit seine Wahl zu ändern.
Zu welcher der folgenden Optionen würden Sie dem Kandidaten raten?
Der Kandidat sollte wechseln.
Begründung: Bei der ursprünglichen Wahl (und damit auch dann, wenn man bei der Entscheidung bleibt) wird das Auto mit 1/3 Wahrscheinlichkeit gewonnen, denn beim Verstecken hatten alle Türen die gleiche Wahrscheinlichkeit. Beim Wechseln wird genau dann gewonnen, wenn die erste Wahl falsch war, also mit Wahrscheinlichkeit 2/3.

