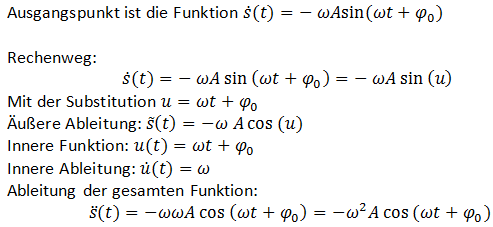Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Der harmonische Oszillator am Beispiel eines Federpendels Teil 1
Ein kleiner Exkurs zum harmonischen Oszillator:
Der harmonische Oszillator ist ein sehr wichtiges Konzept in der Physik: Mit Hilfe des harmonischen Oszillators lassen sich viele Phänomene in der Physik beschreiben. Ein Beispiel ist die Beschreibung des Federpendels, bei dem eine Masse an einer Feder schwingt, oder der elektromagnetische Schwingkreis, bestehend aus Spule und Kondensator. Auch Molekül- und Gitterschwingungen lassen sich mit Hilfe des harmonischen Oszillators beschreiben. Wesentliche Bestandteile der Festkörperphysik und spektroskopische Eigenschaften von Stoffen können so erklärt werden. In der Quantenphysik wird ein quantisierter harmonischer Oszillator verwendet um quantisierte Zustände zu beschreiben.
Zur Aufgabe:
Diese Aufgabe dient dazu, Ihnen einen Einblick in die Physik zu ermöglichen. Sie beschäftigt sich mit dem harmonischen Oszillator am Beispiel eines Federpendels. Hierbei wird ein idealisiertes Experiment formal beschrieben. Wichtige Größen werden berechnet und anschließend physikalisch gedeutet. Die Aufgabe ist etwas umfangreicher und bietet die Möglichkeit selbst zu knobeln. Lassen Sie sich nicht abschrecken, wenn eine Antwort auf Anhieb nicht richtig ist, sondern versuchen Sie das Ergebnis nachzuvollziehen!
Knobeln Sie gerne und machen Ihnen schwierige Rechnungen Spaß?
Wollen Sie lernen, wie man aus Formeln physikalische Zusammenhänge erkennen kann?
Dann ist für Sie das Studium der Physik genau richtig!
Betrachten Sie ein Federpendel bestehend aus einem Körper der Masse m, welcher an einer Feder mit einer Federkonstante k hängt. (Hierbei handelt es sich um ein ideales Pendel ohne Reibung.) Wird das Pendel aus seiner Ruhelage um die Stecke A ausgelenkt und dann losgelassen, so beginnt dieses um seine Ruhelage zu schwingen.
Die Funktion s(t)
Betrachtet man die Bewegung der Masse m in Abhängigkeit der Zeit t, so ist zu erkennen, dass die Bewegung zum Beispiel mit Hilfe der Cosinusfunktion beschrieben werden kann. Wird das Pendel aus seiner Ruhelage (s=0) um die Stecke A ausgelenkt und dann losgelassen, so beginnt es um seine Ruhelage zu schwingen.
Der Ort der Masse des Federpendels s wird als Funktion der Zeit t durch folgende Gleichung beschrieben: s(t) =Acos(ωt+φ0).
Hierbei sind A die (konstante) Amplitude, φ0 die (konstante) Anfangsphase (= 0 wenn das Pendel zum Zeitpunkt t = 0 losgelassen wurde), ω die (konstante) Kreisfrequenz (= Winkelgeschwindigkeit) und t die Zeit.
Aufgabe: Bilden Sie die ersten beiden Ableitungen von s nach der Zeit t und markieren Sie die richtige Antwort. Schnappen Sie sich hierfür Zettel und Stift und los geht’s!
Die erste zeitliche Ableitung
Die Ableitung wird mit Hilfe der Kettenregel gebildet. Dazu werden die äußere und innere Ableitung gebildet und miteinander multipliziert.
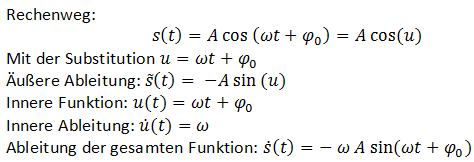
Unabhängig davon, ob Sie die Aufgabe lösen konnten, überlegen Sie sich, ob Ihnen die Art dieser Aufgabe gefällt. Im Physikstudium gibt es viele Umformungen, die man berechnet. Zunächst erscheint dabei alles wie ein großes Buchstaben- und Zeichenwirrwarr. Wichtig ist hierbei zu überlegen, nach welcher Variablen abgeleitet wird (hier die Zeit t), welche Variablen von der Zeit abhängen und welche zeitlich konstant sind. Dabei sollte man sich nicht abschrecken lassen, wie die einzelnen Variablen bezeichnet werden oder wie lang die Formel ist, sondern ruhig und strukturiert vorgehen. Dazu müssen die Grundlagen der Differential- und Integralrechnung sicher beherrscht werden. Um diese vor dem Studium zu vertiefen, wird an der Freien Universität Berlin ein Brückenkurs angeboten.
Interpretation der Formeln
Aufgabe: Deuten Sie die erste und zweite zeitliche Ableitung des Ortes physikalisch. Worum handelt es sich bei den errechneten Größen? Ordnen Sie dazu den beiden Formeln jeweils einen der aufgeführten Begriffe zu.
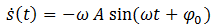
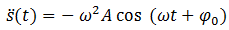
Die zeitliche Änderung des Ortes eines Körpers wird durch die Geschwindigkeit v des Körpers beschrieben. Die zeitliche Änderung der Geschwindigkeit (zweifache zeitliche Ableitung des Ortes) eines Körpers wird durch dessen Beschleunigung a beschrieben. Mit anderen Worten: Die zeitliche Änderung des Ortes entspricht der Geschwindigkeit und die zeitliche Änderung der Geschwindigkeit der Beschleunigung.
Im Physikstudium werden Sie sich mit der physikalischen Bedeutung von Formeln auseinandersetzten und lernen diese zu interpretieren. Ziel ist nicht nur die Bedeutung auswendig zu lernen, sondern viel mehr ein Gefühl zu entwickeln und durch logisches Denken Zusammenhänge selbst zu erkennen.
Die Energie des Federpendels
Bei einem Federpendel wird periodisch kinetische Energie in potenzielle Energie umgewandelt. Dabei ist die Gesamtenergie konstant (ideales Pendel mit Vernachlässigung der Reibung).
Betrachten Sie die Schwingungsperiode des Federpendels.
Wann ist die kinetische Energie EKin maximal?
Wann ist die potenzielle Energie EPot maximal?
Aufgabe: Ordnen Sie die Begriffe am rechten Rand den entsprechenden Punkten im Diagramm zu. Dabei können Sie die Begriffe per Drag & Drop an die entsprechende Stelle ziehen.
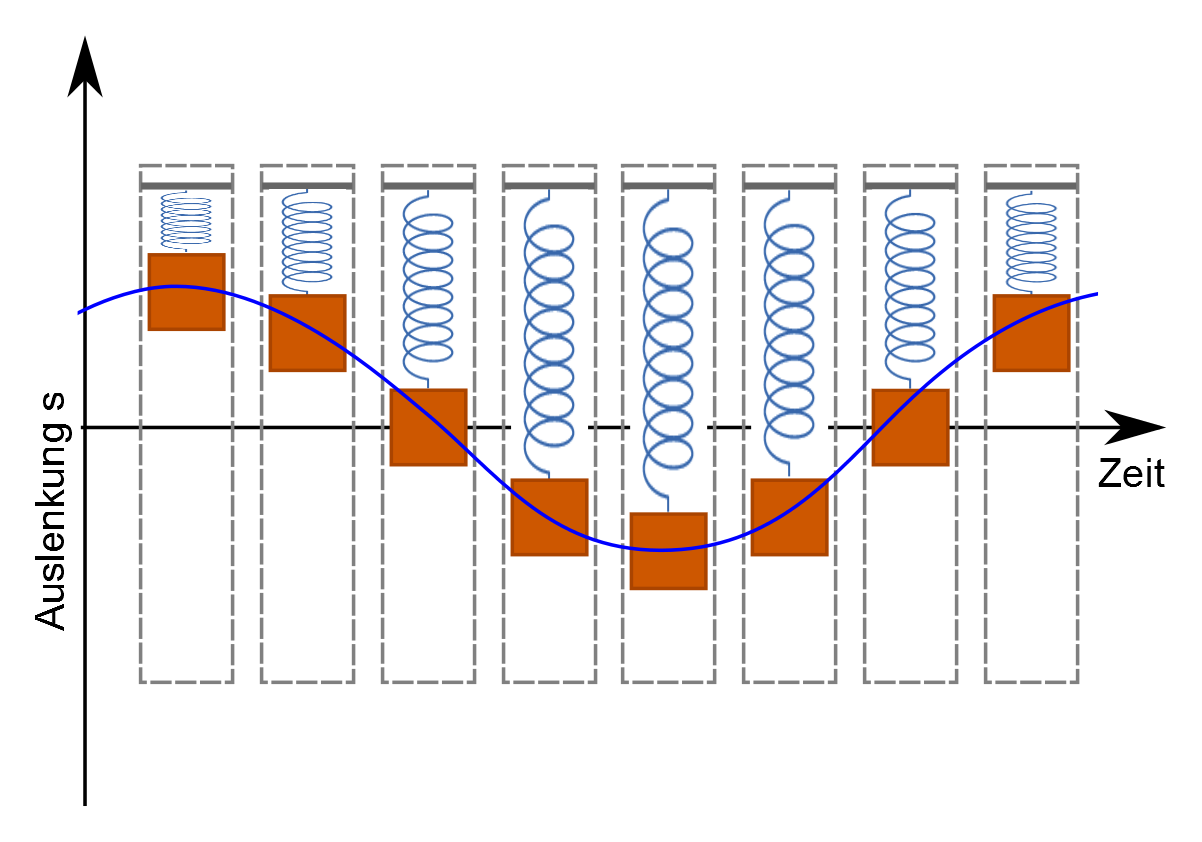
Maximale potenzielle Energie
Maximale kinetische Energie
Ist die Feder des Pendels maximal gestaucht oder gestreckt, so ist die potenzielle Energie des Pendels am größten. Durchquert das Pendel seine Ruhelage, so ist die Geschwindigkeit des Pendels maximal. Die kinetische Energie hängt von der Geschwindigkeit ab und ist folglich an dieser Stelle ebenfalls maximal. Kinetische und potentielle Energie werden periodisch ineinander umgewandelt. Die Gesamtenergie des Pendels bleibt dabei konstant.