Diese Seiten können nicht richtig dargestellt werden, da Sie Ihren Internet Explorer mit aktivierter Kompatibiltätsansicht verwenden. Wir empfehlen 'fu-berlin.de' aus der Liste der Websites mit aktivierter Kompatibilitätsansicht zu entfernen:
- Blenden Sie bitte in Ihrem Internet Explorer die Menüleiste ein, indem Sie entweder 'Alt' drücken oder in der Adressleiste mit der rechten Maustaste klicken und dann 'Menüleiste' auswählen.
- Klicken Sie auf 'Extras' und wählen das Menü 'Einstellungen der Kompatibilitätsansicht' aus.
- Wählen Sie unter 'Zur Kompatibilitätsansicht hinzugefügte Websites' 'fu-berlin.de' aus.
- Klicken Sie auf 'Entfernen'.
Vollständige Induktion
Die vollständige Induktion ist eine typische Beweismethode in der Mathematik. Sie wird angewandt, wenn eine Aussage, die von einer natürlichen Zahl n ≥ 1 abhängig ist, bewiesen werden soll. Wenn also die von den natürlichen Zahlen abhängige Aussage getroffen wird:
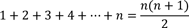
Dann ist das in Wirklichkeit nicht eine Aussage, sondern es sind unendlich viele Aussagen, nämlich die, dass diese Gleichheit für n = 1 gilt und für n = 2 und für n = 27 und für n = 385746, also für alle natürlichen Zahlen. Man könnte nun anfangen, der Reihe nach zu überprüfen, ob das stimmt. Dann wird aber schnell deutlich, dass man das Ganze nicht an allen Zahlen prüfen kann. Selbst, wenn es bei den ersten 5000 Versuchen geklappt hat, bedeutet es nicht, dass es für alle weiteren Zahlen funktioniert. Wir müssen also eine Möglichkeit finden, für alle Zahlen gleichzeitig zu überprüfen, ob die Aussage stimmt.
Hierzu hilft uns die Beweisführung der vollständigen Induktion. Diese Art der Beweisführung läuft immer nach dem gleichen Schema ab. Zuerst wird die getroffene Aussage anhand eines Beispiels überprüft. Dies nennt man „Induktions-Anfang“. Hierfür nimmt man sich das einfachste Beispiel, also meistens n = 1.
Beispiel
Induktionsanfang: n = 1
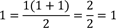
Richtig. Für n = 1 stimmt die Aussage.
Wie gesagt, können wir jetzt nicht unendlich lange weiterprüfen ob es für jede Zahl stimmt. Darum kommen wir nun zum zweiten und sehr entscheidenden Schritt in der Beweisführung, dem „Induktionsschritt“.
Wir nehmen nun an, wir hätten irgendeine Zahl n gefunden, für die die Aussage stimmt
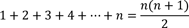
Nun überprüfen wir, ob die Aussage auch für den Nachfolger von n, also für die Zahl n+1 ebenso gültig ist.
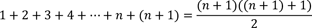
Oder vereinfacht:
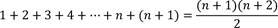
Induktionsschritt:
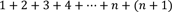
Da wir die Summe der ersten n Zahlen schon aus der Voraussetzung kennen, können wir sie nun einsetzen.
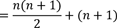
Nun erweitern wir den Summanden (n+1).
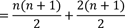
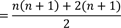
Jetzt können wir die Klammern auflösen.
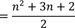
Hier kann man mit Hilfe der Linearfaktorzerlegung wieder Faktoren bilden.
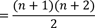
Wir sehen nun, dass:
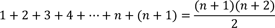
Dies ist genau, was wir herausfinden wollten, nämlich, dass die angegebene Formel, wenn sie für n gilt, auch für seinen Nachfolger (n+1) gilt.
Was bedeutet das für uns? Wenn wir also eine Zahl haben, für die die Aussage gilt, wissen wir nun, dass sie auch für ihren Nachfolger gilt. Glücklicherweise wissen wir durch den Induktionsanfang, dass die Aussage für n = 1 gilt. Durch den Induktionsschritt wissen wir, dass dann auch die Formel für den Nachfolder von n = 1 also für (n+1) = 2 gilt. Wenn die Aussage nun auch für 2 gilt, gilt sie somit auch für den Nachfolger von 2 und den Nachfolger davon usw.. Damit haben wir in nur zwei Schritten bewiesen, dass die Aussage tatsächlich für alle natürlichen Zahlen gilt.
So funktioniert das Konzept der vollständigen Induktion. Zuerst findet man ein Beispiel, bei dem die Aussage stimmt (Induktionsanfang) und dann zeigt man im Induktionsschritt, dass, wenn man eine Zahl hat, bei der die Aussage zutrifft, sie ebenso beim Nachfolger zutrifft. Damit ist der Beweis komplett.
Aufgabe — Darstellung von geraden und ungeraden Zahlen
Alle geraden Zahlen lassen sich durch 2 teilen, alle ungeraden Zahlen nicht. Wenn wir also eine beliebige gerade Zahl benennen möchten, schreiben wir einfach (2k). Wenn wir eine beliebige ungerade Zahl benennen möchten, schreiben wir (2k-1).
Beweisen Sie mit der vollständigen Induktion, dass die Summe der ungeraden Zahlen von 1 bis (2n – 1) gleich n2 sind.
Mathematisch geschrieben sieht das so aus:

1. Induktionsanfang
Nehmen Sie sich ein einfaches Beispiel, wie n = 1.
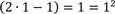
2. Induktionsschritt
Hier setzen wir voraus, dass die Aussage für n stimmt, also
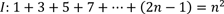
und überprüfen, ob sie dann auch für (n+1) gilt.
Also ob:
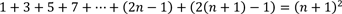
Erklärung: auf der linken Seite haben wir der Summe noch das nachfolgende Glied von (2n - 1) hinzugefügt, nämlich (2(n + 1) – 1). Auf der rechten Seite müsste dann (n + 1)2 herauskommen, was nun zu überprüfen ist.
Wir wissen, aufgrund unserer Annahme, dass I stimmt, dass gilt
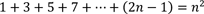
Nun fügen wir das nachfolgende Glied (2(n + 1) – 1) hinzu und erhalten:
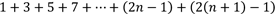
Diesen Term können wir nun umformen und vereinfachen.
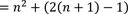
Nun können wir die Klammern auf der linken Seite auflösen:
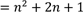
Und schließlich sehen wir hier die erste binomische Formel und können sie rückwärts anwenden in:
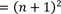
Somit haben wir gezeigt, dass tatsächlich gilt:
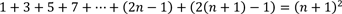
Und der Beweis ist komplett. ▢

